Strip plot analysis using R
 |
| See Video ⮞ ☝ |
AGRON Stats Lectures
June 26, 2018
Introduction
In this tutorial you will learn how to carry out statistical analysis for strip plot or split block design using R program. Strip plot design is specifically suited for a two factor experiment. In this design, the desired precision for measuring the interaction effect between the two factors is higher than that for measuring the main effect of either one of the two factors. This is accomplished with the use of three plot sizes:
- Vertical strip plot for the first factor also called the vertical factor.
- Horizontal strip plot for the second factor also called the horizontal factor.
- Intersection plot for the interaction between the two factors.
The vertical strip and horizontal strip plot are always perpendicular to each other. However, there is no relationship between their sizes, unlike the case of main plot and sub plot of the split plot design.
In this case the interaction plot is of course the smallest.Layout vertical and horizontal strips
Thus in strip plot design, the degrees of precision associated with the main effects of both factors are sacrificed in order to improve the precision of the interaction effect. In the split plot design the levels of second factor are independently randomized within the sub plots of each level of first factor.
In the strip plot design the levels of one factor are assigned to strip plots in one direction and the levels of the second factor to the strips perpendicular to the first strip. A separate randomization is done for each block for each factor A and B.
This design facilitates the physical operations and increases the precision for estimation of interaction effect.Example data set
The example used here is comprised of three varieties and four different fertilizer levels. If varieties are kept in main plots and fertilizer levels in sub plots then the given layout for one block indicates the difference between a split plot and a strip plot design.
Difference between strip and split plot layout
Let’s start how to carry out analysis of strip plot design in R studio.Import data
I often recommend to first clear all the objects or values in global environment using rm(list = ls(all = TRUE)) before importing the data set. You can also clear the plots using graphics.off() and clear everything in console using shell() function.
Now let’s import the data set using read.csv() function. I have already saved the data file as CSV (comma delimited) in the working directory. The file argument specify the file name with extension (data-strip.csv) CSV. In header argument you can set a logical value that will indicate whether the data file contains variable names as first row. In my data set the file contains the variable names in the first row, so I shall use TRUE for this argument. The head() function will print the first six rows of the data set.
# block varieties fertilizer yield
# 1 1 V1 F1 10.2
# 2 1 V1 F2 11.1
# 3 1 V1 F3 6.8
# 4 1 V1 F4 5.3
# 5 1 V2 F1 8.0
# 6 1 V2 F2 9.7The str() or structure function will tell us the format for each column in the data frame. It gives information about rows and columns. It also gives information whether the variables are being read as integer, character, factor or number. In some cases, we may have a variable coded as character or integer that we would like R to recognize as a factor variable. For this purpose as.factor() function is used. In our data file the varieties and fertilizer are being read as character in R instead of being recognized as factor variables.
To change it to factor apply the function of as.factor() where x argument represent the factor component of the data set (data$varieties). This will change the structure of the variable varieties and R will recognize it as factor.
Similarly, assign the same function for second variable by replacing varieties with fertilizer in previous command. Now using again the str() function will show the second variable is being read as factor.
# 'data.frame': 48 obs. of 4 variables:
# $ block : int 1 1 1 1 1 1 1 1 1 1 ...
# $ varieties : Factor w/ 3 levels "V1","V2","V3": 1 1 1 1 2 2 2 2 3 3 ...
# $ fertilizer: Factor w/ 4 levels "F1","F2","F3",..: 1 2 3 4 1 2 3 4 1 2 ...
# $ yield : num 10.2 11.1 6.8 5.3 8 9.7 8.6 3.4 2 10.9 ...# 'data.frame': 48 obs. of 4 variables:
# $ block : int 1 1 1 1 1 1 1 1 1 1 ...
# $ varieties : Factor w/ 3 levels "V1","V2","V3": 1 1 1 1 2 2 2 2 3 3 ...
# $ fertilizer: Factor w/ 4 levels "F1","F2","F3",..: 1 2 3 4 1 2 3 4 1 2 ...
# $ yield : num 10.2 11.1 6.8 5.3 8 9.7 8.6 3.4 2 10.9 ...Fit analysis of variance model
The strip-plot design is specifically suited for a two-factor experiment in which the desired precision for measuring the interaction effects between the two factors is higher than that for measuring the main effect. The variance analysis of a strip-plot design is divided into three parts:
- The horizontal-factor analysis
- The vertical-factor analysis
- The interaction analysis
For analysis strip.plot() function is used to fit the analysis of variance model. This function requires some arguments. The argument BLOCK specify the replications or block variable. In COL argument specify the factor column as varieties in this case. The ROW argument specify the row factor as fertilizer in this case. The last argument Y specify response variable as yield in this case.
attach(data)
library(agricolae)
model = strip.plot(BLOCK = block,
COL = varieties,
ROW = fertilizer,
Y = yield)#
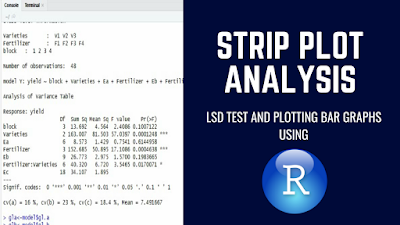
# ANALYSIS STRIP PLOT: yield
# Class level information
#
# varieties : V1 V2 V3
# fertilizer : F1 F2 F3 F4
# block : 1 2 3 4
#
# Number of observations: 48
#
# model Y: yield ~ block + varieties + Ea + fertilizer + Eb + fertilizer:varieties + Ec
#
# Analysis of Variance Table
#
# Response: yield
# Df Sum Sq Mean Sq F value Pr(>F)
# block 3 13.692 4.564 2.4086 0.1007122
# varieties 2 163.007 81.503 57.0397 0.0001248 ***
# Ea 6 8.573 1.429 0.7541 0.6144958
# fertilizer 3 152.685 50.895 17.1086 0.0004638 ***
# Eb 9 26.773 2.975 1.5700 0.1983665
# fertilizer:varieties 6 40.320 6.720 3.5465 0.0170071 *
# Ec 18 34.107 1.895
# ---
# Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#
# cv(a) = 16 %, cv(b) = 23 %, cv(c) = 18.4 %, Mean = 7.491667Yield is significantly affected by both main and interaction effects.LSD mean comparison test
I shall use LSD.test() to compute the significant differences among the mean values. This test create multiple comparisons of treatments by means of LSD and a grouping of treatments. The argument y specify model (aov or lm) or response variable name.
The trt argument represent vector of treatments applied to each experimental units. The value for this argument can be specified either as varieties, fertilizer or varieties:fertilizer where former two represent main factors and last one represent the interaction term. Set the value of error degree of freedom for DFerror argument with respect to each term. This value can be specified by using model$gl.a, model$gl.b and model$gl.c for varieties, fertilizer and interaction term, respectively.
The argument alpha specify the risk level for this test. The default value for this argument in 0.95 representing 5% risk level. In method argument (p.adj) for adjusting probability value, I shall use bonferroni which is most commonly used method. Set a logical value for group argument to specify grouping of treatment means. Set a logical value for console argument to print the outputs.
# Main effects
library(agricolae)
# First factor variable (varieties)
LSD_A = LSD.test(y = yield,
trt = varieties,
DFerror = model$gl.a,
MSerror = model$Ea,
alpha = 0.05,
p.adj = "bonferroni",
group = TRUE,
console = TRUE)#
# Study: yield ~ varieties
#
# LSD t Test for yield
# P value adjustment method: bonferroni
#
# Mean Square Error: 1.428889
#
# varieties, means and individual ( 95 %) CI
#
# yield std r LCL UCL Min Max
# V1 9.025 2.217055 16 8.293764 9.756236 4.6 12.3
# V2 8.550 2.279474 16 7.818764 9.281236 3.4 12.0
# V3 4.900 2.880741 16 4.168764 5.631236 0.9 10.9
#
# Alpha: 0.05 ; DF Error: 6
# Critical Value of t: 3.287455
#
# Minimum Significant Difference: 1.389358
#
# Treatments with the same letter are not significantly different.
#
# yield groups
# V1 9.025 a
# V2 8.550 a
# V3 4.900 b# Second factor variable (fertilizer)
LSD_B = LSD.test(y = yield,
trt = fertilizer,
DFerror = model$gl.b,
MSerror = model$Eb,
alpha = 0.05,
p.adj = "bonferroni",
group = TRUE,
console = TRUE)#
# Study: yield ~ fertilizer
#
# LSD t Test for yield
# P value adjustment method: bonferroni
#
# Mean Square Error: 2.974815
#
# fertilizer, means and individual ( 95 %) CI
#
# yield std r LCL UCL Min Max
# F1 8.483333 3.193981 12 7.357012 9.609654 2.0 12.3
# F2 9.416667 1.407017 12 8.290346 10.542988 6.5 11.2
# F3 7.408333 2.888365 12 6.282012 8.534654 2.2 10.3
# F4 4.658333 2.349258 12 3.532012 5.784654 0.9 7.6
#
# Alpha: 0.05 ; DF Error: 9
# Critical Value of t: 3.364203
#
# Minimum Significant Difference: 2.368845
#
# Treatments with the same letter are not significantly different.
#
# yield groups
# F2 9.416667 a
# F1 8.483333 a
# F3 7.408333 a
# F4 4.658333 b# Interaction (varieties:fertilizer)
LSD_AB = LSD.test(y = yield,
trt = varieties:fertilizer,
DFerror = model$gl.c,
MSerror = model$Ec,
alpha = 0.05,
p.adj = "bonferroni",
group = TRUE,
console = TRUE)#
# Study: yield ~ varieties:fertilizer
#
# LSD t Test for yield
# P value adjustment method: bonferroni
#
# Mean Square Error: 1.894815
#
# varieties:fertilizer, means and individual ( 95 %) CI
#
# yield std r LCL UCL Min Max
# V1:F1 11.175 1.1870833 4 9.7290165 12.620983 10.1 12.3
# V1:F2 9.725 1.0436315 4 8.2790165 11.170983 8.6 11.1
# V1:F3 9.025 1.5305228 4 7.5790165 10.470983 6.8 10.3
# V1:F4 6.175 1.4453950 4 4.7290165 7.620983 4.6 7.5
# V2:F1 9.375 1.9465782 4 7.9290165 10.820983 7.8 12.0
# V2:F2 9.775 1.3937360 4 8.3290165 11.220983 7.9 11.2
# V2:F3 9.425 0.5909033 4 7.9790165 10.870983 8.6 10.0
# V2:F4 5.625 2.1360009 4 4.1790165 7.070983 3.4 7.6
# V3:F1 4.900 2.0896571 4 3.4540165 6.345983 2.0 6.7
# V3:F2 8.750 1.8266545 4 7.3040165 10.195983 6.5 10.9
# V3:F3 3.775 1.1786291 4 2.3290165 5.220983 2.2 4.9
# V3:F4 2.175 1.0242884 4 0.7290165 3.620983 0.9 3.4
#
# Alpha: 0.05 ; DF Error: 18
# Critical Value of t: 4.04629
#
# Minimum Significant Difference: 3.93845
#
# Treatments with the same letter are not significantly different.
#
# yield groups
# V1:F1 11.175 a
# V2:F2 9.775 ab
# V1:F2 9.725 ab
# V2:F3 9.425 abc
# V2:F1 9.375 abc
# V1:F3 9.025 abc
# V3:F2 8.750 abcd
# V1:F4 6.175 bcde
# V2:F4 5.625 cdef
# V3:F1 4.900 def
# V3:F3 3.775 ef
# V3:F4 2.175 fCompute mean and standard error
Before visualizing main and interaction effects first compute mean values and standard error. Load the library dplyr that states the grammar of data manipulation. Connect data set to group it by first varieties and then summarise it to get mean values and standard error using group_by() and summarise() function, respectively. For connection we shall use %>% pipe operator. In function summarise() set functions for the objects avg_A and se to compute mean and standard error values. Print function will display the results for this object.
Similarly, get mean values and standard error for second variable factor using the same command except connecting the data set to group_by() fertilizer using %>% pipe operator. Print function for this object will display the results. Again use the same command for interaction term. Here you will connect the data set to group_by() varieties and fertilizer using the %>% pipe operator. Print function for this object will display the results. Attach these three objects to access its components by simply giving their names while visualizing plots.
# For main effects
library(dplyr)
MeanSE_A = data %>%
group_by(varieties) %>%
summarise(avg_A = mean(yield),
se = sd(yield)/sqrt(length(yield)))
MeanSE_B = data %>%
group_by(fertilizer) %>%
summarise(avg_B = mean(yield),
se = sd(yield)/sqrt(length(yield)))
# For interaction
MeanSE_AB = data %>%
group_by(varieties, fertilizer) %>%
summarise(avg_AB = mean(yield),
se = sd(yield)/sqrt(length(yield)))
print(MeanSE_A)# # A tibble: 3 x 3
# varieties avg_A se
# <fct> <dbl> <dbl>
# 1 V1 9.02 0.554
# 2 V2 8.55 0.570
# 3 V3 4.9 0.720# # A tibble: 4 x 3
# fertilizer avg_B se
# <fct> <dbl> <dbl>
# 1 F1 8.48 0.922
# 2 F2 9.42 0.406
# 3 F3 7.41 0.834
# 4 F4 4.66 0.678# # A tibble: 12 x 4
# # Groups: varieties [3]
# varieties fertilizer avg_AB se
# <fct> <fct> <dbl> <dbl>
# 1 V1 F1 11.2 0.594
# 2 V1 F2 9.72 0.522
# 3 V1 F3 9.02 0.765
# 4 V1 F4 6.18 0.723
# 5 V2 F1 9.38 0.973
# 6 V2 F2 9.78 0.697
# 7 V2 F3 9.43 0.295
# 8 V2 F4 5.62 1.07
# 9 V3 F1 4.9 1.04
# 10 V3 F2 8.75 0.913
# 11 V3 F3 3.78 0.589
# 12 V3 F4 2.17 0.512Visualize effects
Plot varieties
Let’s start to display the main and interaction effects using grammar of graphics ggplot() function. This will require to load the package ggplot2 by using library() function.
Create an object p1 using the grammar of graphics function. This function requires data set (MeanSE_A) and some aesthetic mappings to use for the plot. In aesthetic mappings function the argument x specify the variable varieties and argument y specify mean values (avg_A) for response variable that is yield. Print function will print a blank plot showing x-axis and y-axis labels.
Now let’s add layers to this plot object. For plotting bars use geom_bar() function. In stat argument set the value as identity to leave the data as is. In color argument specify the color for borders of the bars. The position argument specify the Position adjustment, either as a string, or the result of a call to a position adjustment function. The argument width specify the width of the bars. Printing this layer with plot object will display bars on the plot.
Let’s add the second layer to show error bars on the bars of the plot. For this use geom_errorbar() function. In aesthetic mappings you can specify the maximum ymax and minimum ymin values to show the heights of the error bars. Use the same position argument as used in previous command so that the error bars could place in the center of the bars. You can adjust width of the error bars by setting the value for width argument.
Let’s change the main title, X and Y axis labels of the plot. For this use labs() function. In title you can specify the main title of the plot. For x and y argument specify the labels to be used for x-axis and y-axis.
library(ggplot2)
# Create plot object
p1 = ggplot(MeanSE_A, aes(x = varieties,
y = avg_A))
# Adding layers to p2 object
# Adding bars
plotA = p1 +
geom_bar(stat = "identity",
color = "black",
position = position_dodge(width=0.9))
# Adding error bars
plotB = plotA +
geom_errorbar(aes(ymax = avg_A + se,
ymin = avg_A - se),
position = position_dodge(width=0.9),
width = 0.25)
# Changing main title, X and Y labels
plotC = plotB +
labs(title = "",
x = "varieties",
y = "yield")Plot gender
The same functions will be used to plot bar graph for second factor. For plotting fertilizer first create an object p2 using grammar of graphics function. Use same arguments in this object changing the values to represent the second factor data set (MeanSE_B). Similarly, use gender for x argument and avg_B for y argument Print function will display the empty plot for this object just showing the X and Y axis labels.
For adding layers to this plot object use the same functions as used in adding layers for first variable factor. Just change the values of the arguments representing factor B instead of factor A. This will result in printing all the layers to the object plot.
# Create plot object
p2 = ggplot(MeanSE_B, aes(x = fertilizer,
y = avg_B))
# Adding layers to p2 object
# Adding bars
plotA = p2 +
geom_bar(stat = "identity",
color = "black",
position = position_dodge(width=0.9))
# Adding error bars
plotB = plotA +
geom_errorbar(aes(ymax = avg_B + se,
ymin = avg_B - se),
position = position_dodge(width=0.9),
width = 0.25)
# Changing main title, X and Y labels
plotC = plotB +
labs(title = "",
x = "fertilizer",
y = "yield")Plot interaction
First create the plot object similar to the one created for main effects. However, you will change the arguments to represent the interaction data set (MeanSE_AB). In aesthetic mappings define x, y and fill arguments. The argument x specify gender or the variable name that you want to place on X axis. In y argument set the mean values for interaction term. The argument fill specify the second factor used to set the color and fill of geom elements on a plot. I shall set the varieties for this argument. Print function will display the empty plot for this object just showing the x-axis and y-axis labels.
Now add the layers to this plot object. Use same arguments for geom_bar() as used in previous command to plot bars except replacing the values of arguments to represent the interaction term instead of main effects.
Now I shall type a different layer for adding color for fill and changing legend text. For this use scale_fill_manual() function. In values argument set the fill color for the bars. In labels you can specify labels for the legend text. Print function for this layer will add fill color and labels for legend text.
To add error bars on top of the plot bars use geom_errorbar() function. You can specify settings for aesthetic mappings (aes()), position and width of the error bars. In aesthetic mapping set the maximum ymax and minimum ymin values for error bars on Y axis. I shall set these values by adding (avg_AB + se) and subtracting (avg_AB - se) standard error from height of the bars. Specify position argument same as used in previous command (commond for plotting bars geom_bar()). This will result placing the error bars exactly on the same position as the bars were plotted. You can change the width of the error bars by setting the value for width argument. Printing this layer will add error bars.
To add main title, x and y labels use the same arguments as used in previous commands while plotting main effects. An additional fill argument can be specified for legend title. Printing this layer will add main title, X-axis and Y-axis labels and legend title to the plot.
library(ggplot2)
# Create plot object
p3 = ggplot(MeanSE_AB, aes(x = fertilizer,
y = avg_AB,
fill = factor(varieties)))
# Adding layers to plot object
# Plotting bars
plotA = p3 +
geom_bar(stat = "identity",
color = "black",
position = position_dodge(width=0.9))
# Adding color for fill and changing legend text
plotB = plotA +
scale_fill_manual(values = gray(1:3/3),
labels = c("Super", "Shaheen", ("Basmati-15")))
# Adding error bars
plotC = plotB +
geom_errorbar(aes(ymax = avg_AB + se,
ymin = avg_AB - se),
position = position_dodge(width=0.9),
width = 0.25)
# Changing main title, X and Y labels and legend title
plotD = plotC +
labs(title = "",
x = "fertilizer",
y = "yield",
fill = "varieties")For additional command on how to place alphabets from mean comparison test on the top of error bars please —
visit_here.For a video tutorial please —
click_here.
Please comment below if you have any questions.
Download data file — Click_here
Download Rscript — Download Rscript
Download R program —
Click_hereDownload R studio —
Click_here



What is the difference between casino games and slots?
ReplyDeleteSlot games are the 우리 카지노 계열사 most popular 메리트카지노 가입쿠폰 types of casino games, and the majority 카지노 사이트 are slots. and 개집 왕 the most 더킹카지노 슬롯 commonly played slot games.